This page last modified 2016 October 04
Twilight
Questions about the twilight arise regularly on astronomy newsgroups. This
document is an attempt to answer some of these questions.
What is Twilight?
Twilight is the period between the Sun disappearing behind the horizon and the sky becoming fully dark (light pollution excepted, of course). Twilight is divided into three phases:
- Civil Twilight: The geometric centre of the Sun is between 0o and 6o below the horizon. Assuming a clear sky and atmosphere, the brightest stars and the planets Venus and Jupiter may be visible, objects still have their colours and there is sufficient light to enable normal daylight activities.
- Nautical Twilight: The geometric centre of the Sun is between 6o and 12o below the horizon. Assuming a clear sky and atmosphere, more stars and plabets will become visible, but objects will tend to lose their colours fade and become shades of grey as scotopic vision takes over from photopic vision. It is called "nautical" because, between the end of nautical dusk and nautical dawn, it is no longer possible to distinguish between the sky and a sea horizon, so navigational sightings based on a sea horizon are no longer possible. Normal daytime activity on land is not possible and the land horizon becomes indistinct.
- Astronomical Twilight: The geometric centre of the Sun is between 12o and 18o below the horizon. To the casual, non-astronmical observer, twilight has ended (or, in the dawn, not yet started) and night has begun. In the absence of light pollution and given a clear atmosphere, all astronomical observations are possible between dusk astronomical twilight and dawn astronomical twilight.
Why is twilight shorter near the equator?
Twilight depends on the angular distance of the Sun below the horizon. The Sun appears to move along its line of declination. At the equator, lines of declination are perpendicular to the horizon so, after the Earth has rotated 18o after sunset, to a first approximation (i.e. ignoring the curvature of the lines of declination) the Sun will be 18o (or nearly so) below the horizon:
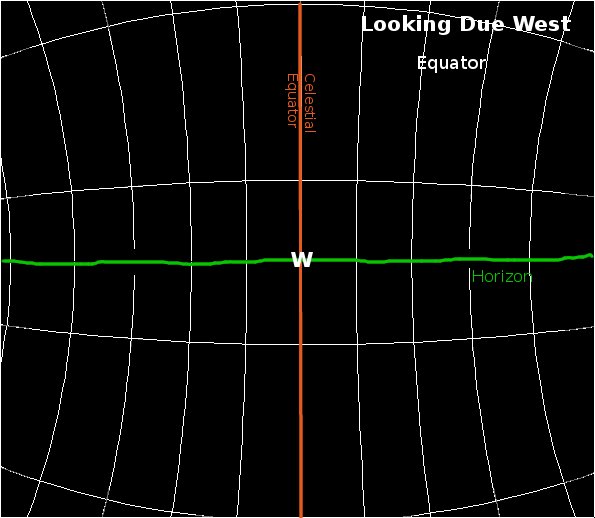
Away from the equator, declination lines intersect the horizon at an angle equal to the co-latitude. E.g. at 51o, they will interesect the horizon at 90o - 51o = 39o:
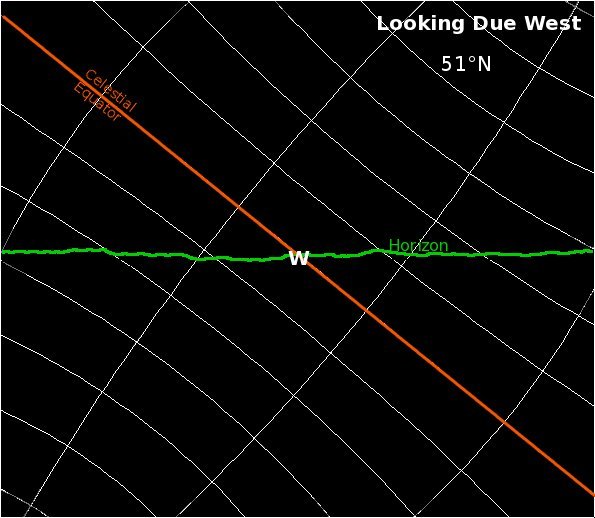
Hence after the Earth has rotated 18o, to a first approximation (i.e. ignoring the curvature of the lines of declination) the Sun will only be 18cos(latitude)o below the horizon. At 51oN, this is 18cos51o = 11o below the horizon.
Away from the equator, declination lines intersect the horizon at an angle equal to the co-latitude. E.g. at 51o, they will interesect the horizon at 90o - 51o = 39o:
Hence after the Earth has rotated 18o, to a first approximation (i.e. ignoring the curvature of the lines of declination) the Sun will only be 18cos(latitude)o below the horizon. At 51oN, this is 18cos51o = 11o below the horizon.
Why is twilight shorter at the equinoxes than at the solstices?
At a first approximation, an easy way to visualise this is to picture the apparent paths of the Sun on the celestial sphere at different times of year. At the equinoxes, the Sun's declination circle is larger than at the equinox, so the Sun has a greater linear speed than at the solstices, so it descends below the horizon more quickly, but the change from winter to summer is even greater.
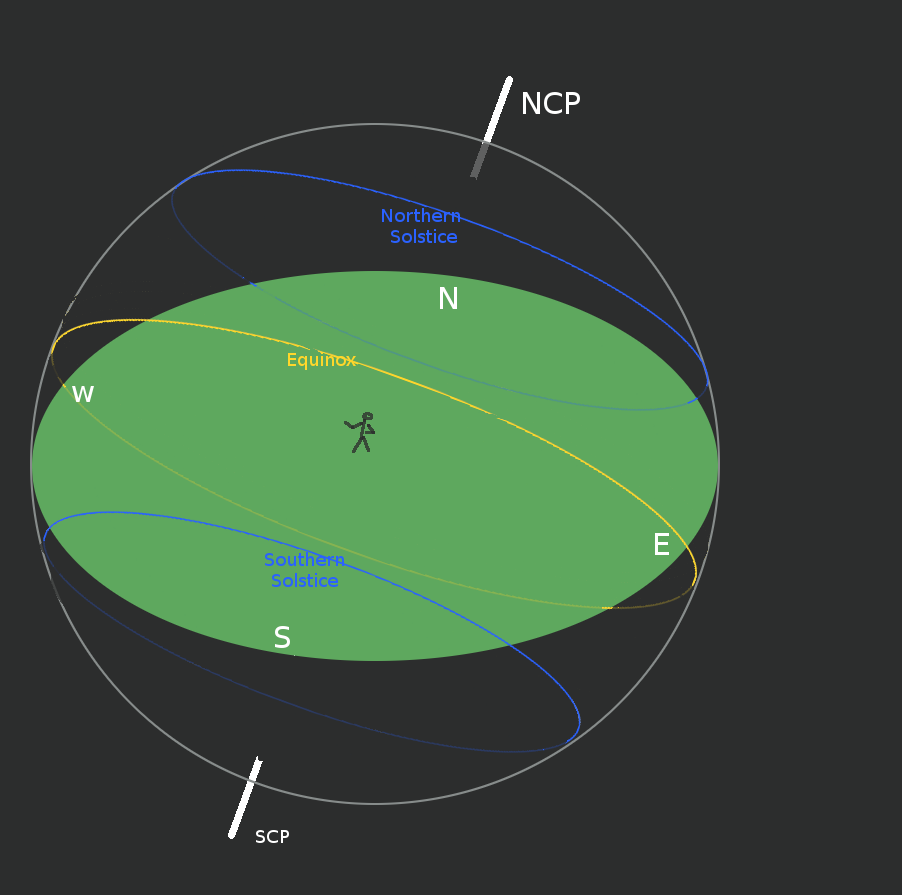
Why is twilight longer in summer than in winter?
Twilight depends on the angle of the Sun below the horizon. The Sun appears to move along its line of declination. In the summer, when the Sun is in the north of the celestial sphere, its declination line curves up towards the horizon:
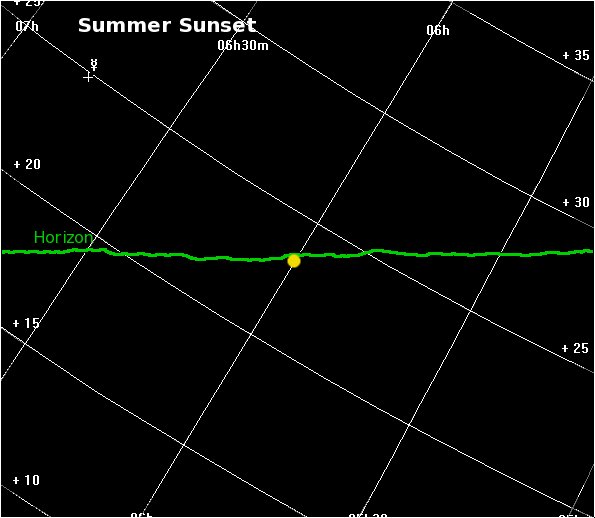
This has the effect of gradually decreasing the angle at which the Sun appears to travel with respect to the horizon, thus increasing the time it takes to attain a given angle below the horizon.
In winter, when the Sun is in the south of the celestial sphere, its declination line curves down away from the horizon. This has the effect of gradually increasing the angle at which the Sun appears to travel with respect to the horizon, thus decreasing the time it takes to attain a given angle below the horizon.



