This page last modified 2001 August 25
The Tides
Questions about the tides arise regularly on astronomy newsgroups. This
document is an attempt to answer some of these questions.
What causes the tides?
Our initial considerations about tides will consider a simple model in which we have a non-rotating Earth that, were it not for tides, would be covered with a uniform depth of water, which exerts no frictional drag. We will add complications like rotation and topography later. This is also a qualitative treatment in which none of the drawings is to scale!
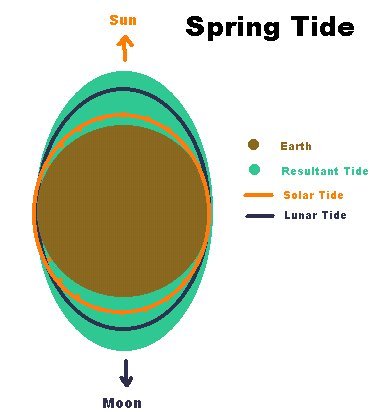
Tides arise as a consequence of the gravitational interaction of the Earth with the Sun and the Moon. That of the Moon is greater than that of the Sun. Most people are aware that at syzygy (when the gravity of the Sun and Moon act in the same line) there are Spring Tides.
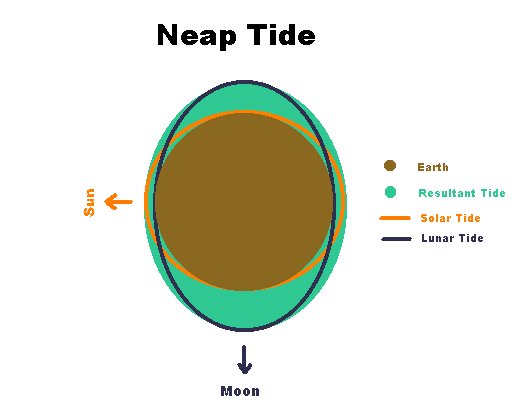
and at quadrature (when the gravity of the Sun and Moon act perpendicularly
to each other) there are Neap Tides:
The Earth rotates beneath the water once per day, thus (in this simple
model) there are two high tides daily.
Also, note that the Moon orbits the
Earth in an elliptical orbit, as does the Earth orbit the Sun. At perigee and
perihelion the gravitational attraction of the Moon and Sun respectively will be
greatest, thus the resulting tides will be higher. The highest spring tides will
occur when the Earth is at or near perihelion and the New or Full Moon is at or
near perigee.
Why are there two tides a day?
This is a question that arises regularly, and is one to which many of the
answers given are either wrong or overly complicated. Before we embark on this
it is necessary to briefly consider frames of reference. Many of the
explanations given for the tidal bulge on the side of the Earth distant from the
Moon invoke an imaginary force called centrifugal force [1].
This is a mathematical construct that permits us to consider a rotational frame
of reference. It is unnecessary; the force that is responsible for raising tides
is the gravitational force. If we consider an inertial frame of reference
we can dispense with the concept of a centrifugal force and simplify things by
considering only real forces.
Imagine the Moon to the right of your
computer screen.
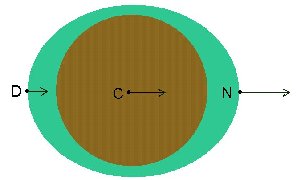 Let's take a line through the centre of the Earth and 3 points
on that line. D is the point on the Earth's ocean surface most distant from the
Moon, N is the point on Earth's ocean surface nearest the Moon, C is the Centre
of the Earth. N is nearest the Moon, so experiences the greater gravitational
pull, D is most distant, so it experiences the least pull, and C experiences a
pull intermediate between the two:
Let's take a line through the centre of the Earth and 3 points
on that line. D is the point on the Earth's ocean surface most distant from the
Moon, N is the point on Earth's ocean surface nearest the Moon, C is the Centre
of the Earth. N is nearest the Moon, so experiences the greater gravitational
pull, D is most distant, so it experiences the least pull, and C experiences a
pull intermediate between the two:
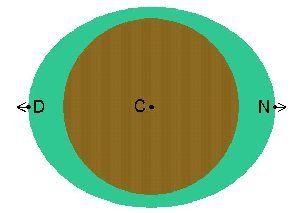
Assuming a rigid Earth [2] cloaked in fluid ocean, there
is a bulge at N because the water there is being pulled more than C and there is
a bulge at D because it is being pulled less than at C. If this doesn't satisfy
you, let's play with the vectors. The arrows on the diagram above are force
vectors. If we subtract the force vector at C from those at D and N, we have:
Hence, relative to the centre of the Earth, the force vectors at D and N are opposite and approximately equal [3], hence 2 tides.
Why isn't the high tide directly underneath the Moon?
There are two components to the answer to this question:
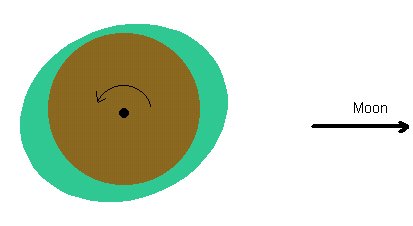 A) If we
desimplify our original model by considering the friction between the body of
the Earth and the sheath of water, we see that the Earth tries to drag the tidal
lumps around with it in its daily rotation, and the Moon tries to retard it. The
result of this is that the tidal bulge 'leads' the Moon [4].
A) If we
desimplify our original model by considering the friction between the body of
the Earth and the sheath of water, we see that the Earth tries to drag the tidal
lumps around with it in its daily rotation, and the Moon tries to retard it. The
result of this is that the tidal bulge 'leads' the Moon [4].
This is further complicated by the relative positions of the Sun and the Moon (see below) that result in variations of the tidal period.
B) If we further complicate our simple model by introducing real topography,
we find that this changes things dramatically. Real tides are also the
consequence of oscillations in the ocean basins, of funnelling into narrow
waterways, of retardation by shallow water, etc. Real tides cannot be predicted
from first principles and need empirical observation for at least a complete
Saros period (i.e. 223 synodic months, after which the Sun and Moon return to
the same positions in the sky) before reasonably reliable predictions can be
made, but even these will be affected by things like barometric pressure.
Why are alternate high tides higher than the intervening ones?
 The short answer is that this is not necessarily the case. When it
does happen a frequent wrong answer that is given is that the tide on
the Moon side of the Earth is higher, and then resorts to a spurious argument
about gravitational attraction and centrifugal forces.
The short answer is that this is not necessarily the case. When it
does happen a frequent wrong answer that is given is that the tide on
the Moon side of the Earth is higher, and then resorts to a spurious argument
about gravitational attraction and centrifugal forces.
The correct
answer is that it is due to the fact of the 23.5° orbital tilt of the
Earth's axis of rotation with respect to the plane of the ecliptic (aka the obliquity
of the ecliptic). The moon's position remains within 5 degrees of the
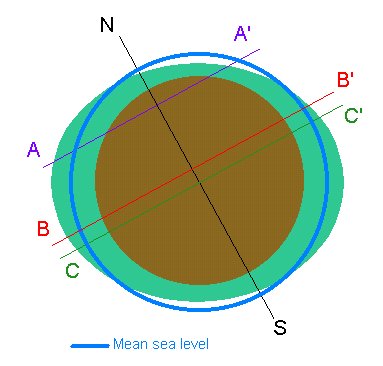
ecliptic. The resulting gross tidal bulges with respect to mean sea level look
like this:
The first thing to note is that at the latitude A, there is only one high
tide per day, because at A' the water opposite the tidal bulge at A is actually
below mean sea level. This is called a diurnal tide.
At
latitude B, the tidal bulges are different heights above mean sea level, with
the tide being higher at a point when it is rotating under B than it is under
B'. This is called a mixed tide.
At latitude C the tidal bulge is
the same height above mean sea level at both C and C'. The tides will therefore
be of approximately the same height. This is a semidiurnal tide.
The difference in height of alternate tides is called 'diurnal
inequality' and is dependent on the declination of the Moon. When the Moon
is south of the (celestial) equator, 'Moon-side' tides in the N hemisphere will
be lower than the other tide; they will be higher when the Moon is N of the
equator.
Why is there so much variation in the tidal period?
There are several reasons for this:
The explanation given above for how the tide
'leads' the Moon is grossly simplified, in that it does not take account of the
Sun. During waxing crescent and waning gibbous phases of the Moon the geometry
is such that the 'lead' is greater – this is called tidal priming.
During the waxing gibbous and waning crescent phases the 'lead' is reduced –
this is called tidal lagging.
Because of the ellipticity and
obliquity of the Moon's orbit, the period between its meridian passage (aka.
culmination, transit) varies, thus varying the length of the tidal day
whose mean is 24h 50min.
The motion of the Moon is (un)reasonably
complicated. Not only does it move in an ellipse whose plane is inclined to that
of the ecliptic, but this orbit is perturbed by the Sun. The changing effect of
the Sun's gravity is called variation. To it must be added
evection and annual inequality. Evection is a change in
the eccentricity of the orbit. Annual inequality is the effect of the
Earth not maintaining a constant distance from the Sun owing to its elliptical
orbit. These perturbations affect the mean anomaly (the angle of an
imaginary mean moon, travelling at constant angular speed in a circular
orbit, from its perigee, measured at the centre of the circle) of the Moon by up
to about 10°. The true anomaly (angle of true Moon, real orbit,
etc.) is a function of the mean anomaly and the eccentricity.
[1] To those who wish to insist that we must consider a rotational frame of reference because we are living in one, I have two things to say:
- Consider the words of Mike Humberston written in the newsgroup
uk.sci.astronomy:
"This is a bit like a person who lives inside a box claiming that the limits of the universe are the edges of his box. Those of us who choose to live outside of boxes can see that he is incorrect." - Get your information about tides here. As you will see, the force diagrams become more complicated in a rotating frame of reference.
[2] In fact the Earth is not rigid. It has approximately the same rigidity as mild steel and the crust experiences tides of the order of a few centimetres in amplitude. We do not notice these because we do not have a point of reference against which to experience them.
[3] The force at N is slightly higher than the force at D, owing to the inverse cube relationship between separation and tidal force. However, this is not the cause of the tidal inequality. There is also a comparatively minuscule tide-raising force resulting from the centripetal acceleration that is due to the Moon and Earth 'orbiting' their barycentre (which is 1600 km deep inside the Earth) with a period of one sidereal month.
[4] A consequence of this is that the Moon is 'dragging' on the Earth, slowing its rotation and increasing the day length by 2 milliseconds per century. The angular momentum of the system is conserved, the Moon's angular momentum increases (or, put another way, it gains rotational energy from Earth as Earth slows) and as a consequence it gradually moves further away.


