This page last modified 1998 July 21
Positional Astronomy
Positions on Earth
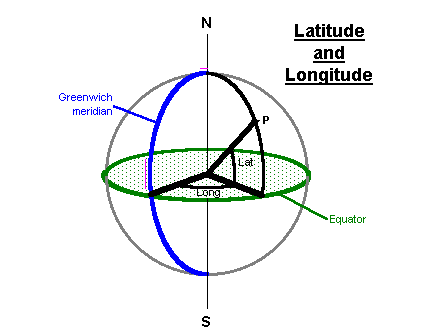
We measure positions on Earth's surface by Latitude and Longitude. Latitude is referred to a reference plane, an imaginary plane which
passes through Earth at the Equator. Longitude is referred to a reference
direction, the meridian which passes through Greenwich.
Positions on the Celestial Sphere
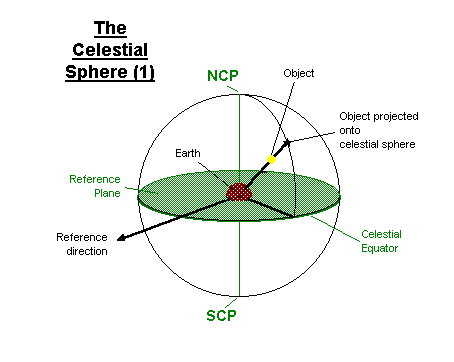
We imagine that astronomical objects are projected onto a celestial sphere,
centred upon Earth. Earth's North and South poles are projected to the North
Celestial Pole (NCP) and South Celestial Pole (SCP) respectively. Earth's
equatorial plane passes through the Celestial Equator, which forms our reference
plane. (The determination of the reference direction will be covered later)
Horizon
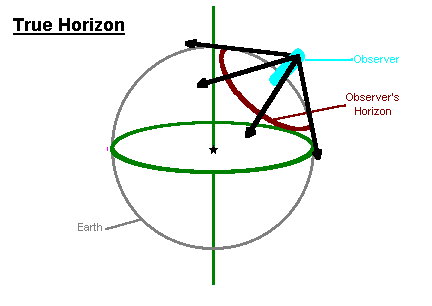
An observer on Earth sees part of the curve of Earth's surface as the
horizon.
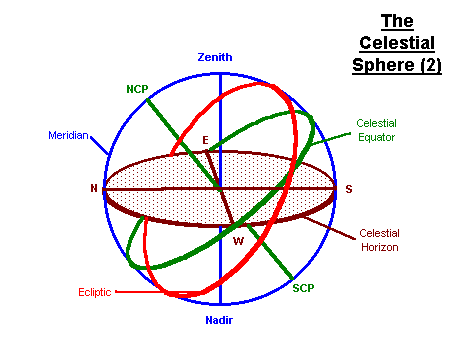
This horizon can also be projected onto the celestial sphere as the
Celestial Horizon. The point directly above the observer is the Zenith; the
point directly below is the Nadir. The observer's compass directions, N, E, S,
W, can also be projected onto this plane. A great circle on the which passes
through N, S and the Zenith is called the Meridian. The meridian also passes
through the NCP and the SCP. The altitude of an object is measured with respect
to the Celestial Horizon; i.e. its reference plane is the horizontal plane.
(Zenith Distance = 90° - altitude) Azimuth is measured through east from
North; i.e. its reference direction is the North point on the horizon.
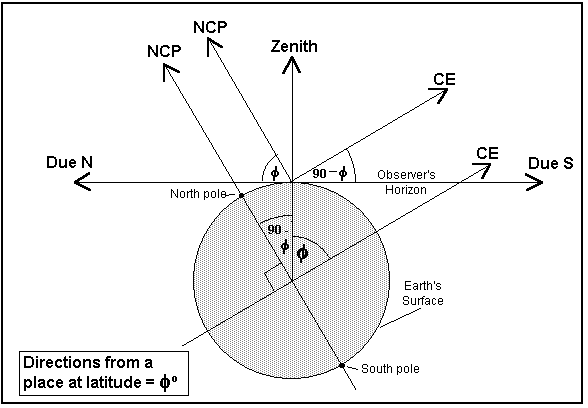
Altitude of Celestial Pole
The altitude of the NCP is equal to the latitude of the observer. The highest altitude of the celestial equator (i.e. due S) is the complement of the latitude.
Equatorial Co-ordinates
Equatorial Co-ordinates are referred to the Celestial Equator as the reference plane and to the First Point of Aries (FPA) as the reference direction. The FPA is the position of the Vernal Equinox; it is where the Ecliptic crosses the Celestial Equator. Owing to the Precession of the Equinoxes, the FPA moves around the equator with a period of about 26,000 years. Equatorial positions must therefore be referred to a date or Epoch. The epoch currently used is AD2000.0
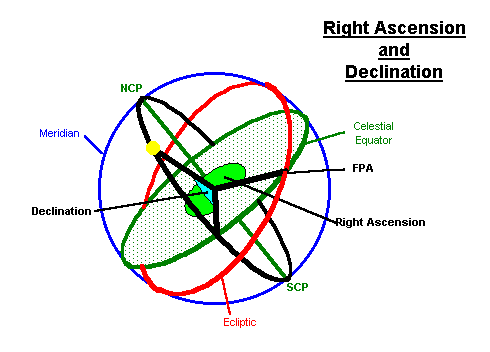
The Declination (Dec) of an object is its position measured northwards from the equatorial plane. It is measured in degrees. Objects south of the equator have negative declinations. Dec is analogous to Latitude.
The Right Ascension (RA) of an object is it's position, measured eastwards around the equator, from the FPA. By convention, the equator is not divided into 360°, but into 24 hours (and minutes and seconds. (The reason for this will become apparent in the section on Sidereal Time.) RA is analogous to Longitude.
The Hour Angle (HA) of an object is its position, measured around the celestial equator, westward from the observer's meridian.
Co-ordinate conversions
Users of altazimuthally mounted instruments often find it useful to be able to convert equatorial co-ordinates to horizon (altitude and azimuth) ones.
r = right ascensionLST = local sidereal time
d = declination
A = azimuth
a = altitude
l = latitude
sin(a) = sin(d) × sin(l) + cos(d) × cos(l) × cos(LST-r)
cos(A) = (sin(d) - sin(l) × sin(a)) / (cos(l) × cos(a))
References
Among the best is Chris Kitchin's excellent Telescopes and Techniques, which is thorough and explains it in clear language.
For detailed accounts of co-ordinate transformations, see Gerald North's chapter in The Modern Amateur Astronomer gives a simple introduction which expands upon the notes given above.


