This page last modified 2003 Aug 04
Barlow Lenses
What is a Barlow Lens?
A Barlow is a negative (diverging) lens that is placed between the objective lens (or primary mirror — from now on these words will be used interchangeably) and the eyepiece of a telescope. It increases the effective focal length of an objective lens, thereby increasing the magnification. The idea is that 2 eyepieces and a Barlow will give you the flexibility of magnification of 4 eyepieces, and will give higher magnifications with less powerful eyepieces.
What are its Advantages and Disadvantages?
Assuming that the Barlow is a good one, the only disadvantage is a slight loss of light throughput — this is of the order of 3%. The advantages are numerous:
- Higher magnifications can be attained with longer focal-length eyepieces than would be possible without the Barlow. Short focal length eyepieces necessarily have optical surfaces that are more curved and therefore are likely to introduce more aberrations.
- A Barlow increases the effective focal ratio of the objective. This gives a
more acute light cone, which is less demanding of eyepiece quality because:
- Rays at the periphery of the cone are closer to being paraxial and thus are less subject to aberration.
- A smaller area of the field lens is used.
- Many eyepieces have an eye relief (distance of exit pupil from eye lens) that is directly related to its focal length. For example, the eye relief of a Plössl is 0.73 × its focal length. Thus, with these eyepieces, for a given magnification there will be greater eye relief with a barlow than without.
- Many eyepiece types do not work well with short focal-ratio objectives. The Barlow effectively increases the focal ratio, allowing the eyepiece to work well.
How does a Barlow work?
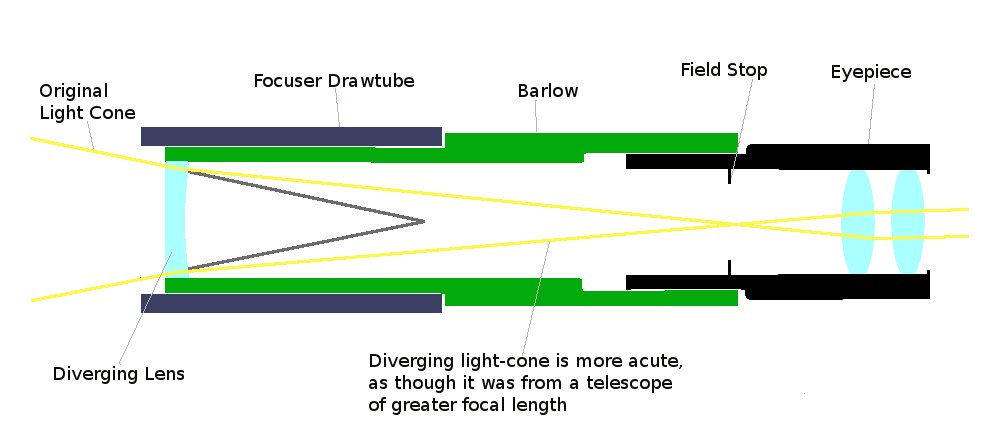
Barlow Amplification
The amplification factor of a Barlow is a function of its position in
relation to the eyepiece and the objective lens (or primary mirror). For any
given eyepiece and objective, the Barlow-eyepiece separation and the
Barlow-objective separation are related because the focal plane of the eyepiece
is the same as the focal plane of the objective-Barlow combination; as the
separation between the eyepiece and the Barlow increases, the separation of the
Barlow and objective decreases.
The amplification factor of a Barlow
can be increased by increasing its separation from the eyepiece using an
extension tube — it must simultaneously be brought closer to the objective.
One thing that you need to watch for with Barlows used outside their
design amplification factor is spherical aberration. SA will be minimised at the
design factor, but will almost certainly be present outside this, although it
may not be discernible. (But visually, using the old trick of shifting the
Barlow to the "other" side of the star diagonal or of using extension
tubes, this may be compensated by reduced SA in the eyepiece, as a
consequence of a more acute light cone.)
Eyepiece Choice
If you use a Barlow with fixed-focus eyepieces, you need to give some
thought to a suitable choice. If, for example, you have a x2 Barlow and a 25mm
eyepiece, there is little point in acquiring a 12.5mm; it will mimic the 25mm +
Barlow. A suitable choice might be 32mm, 18mm, 12mm.
Stop here unless you fancy some basic high school physics & maths.
Barlow Maths
Calculating Barlow magnification:
F = focal length of objective or primary
f = focal length of Barlow [1]
J = joint focal length (effective focal length)
d = separation of Barlow and original focal plane (objective focal
plane)
x = separation of barlow and new focal plane (eyepiece focal
plane)
M = amplification of Barlow
J = (F×f)/(f-d) ...(1) (combined lens formula)
M = J/F ...(2) (by definition)
=
f/(f-d)
The separation of the Barlow and the new focal plane can be calculated from
M and f:
x = f×(M-1) ...(3)
...from which we get :
M = 1 + (x/f)
One of the connotations of all this is that a Barlow that is its own
focal length inside the original focal plane (d) will produce a
collimated (i.e. parallel) beam. Another is that d only needs to
change slightly to bring about significant variations in x (play with
the formulae — or your telescope — to see this) [2].
Finding the approximate Focal Length of a X2 Barlow
The simplest way to do this is as follows:
- Locate the location of the field stop inside an eyepiece.
- Mark this position on the outside of the eyepiece barrel.
- Locate the position of the middle of the lens grouping in the Barlow.
- Mark this position on the outside of the Barlow barrel.
- Insert the eyepiece into the Barlow.
- Measure the distance between the two marks. This is the approximate focal length of the Barlow.
Note: This can only be approximate as the distance of the field stop from the "shoulder" of the eyepiece barrel varies from eyepiece to eyepiece. This is why the marked amplification factor of a Barlow can only be nominal.
Worked examples:
1. Based on Separation of Eyepiece Focal Plane and Barlow
Let us take a 75mm focal length x2 (nominal) Barlow used at its designed
amplification. (f = 75mm, M = 2)
M = 1 + (x/f)
δx = f(M - 1) = 75(2 - 1) mm = 75mm
This
relationship (the separation of Barlow and the new focal plane is equal to the
focal length of the Barlow) holds for any x2 Barlow.
Let us now
use the old trick of increasing Barlow amplification by inserting a star
diagonal between the eyepiece and Barlow. Assume that the star diagonal adds
80mm to the optical path.
M = 1 + (x/f) = 1 + (75 + 80)/75 = 3.07
i.e.
a nominal x2 Barlow has become an (approximate) x3 Barlow. Similarly, the
introduction of a 150mm extension tube instead of the diagonal will give an
amplification factor of x4.
2. Based on Separation of Objective Focal Plane and Barlow.
Let's take a 150mm f/10 objective (F = 1500mm) with a 75mm focal
length Barlow (f) placed 50mm inside focus (d).
Substituting
in equation (1):
J = (F×f)/(f-d)
= (1500 × 75)/(75-50) mm
= 4500mm
Substituting in equation (2):
M = J/F
= 4500/1500
= 3
Hence we have an amplification factor of ×3.
Substituting
in equation (3):
x = f×(M-1)
= 75 × (3 - 1) mm
= 150mm
Using the same objective with the Barlow 37.5mm inside the original
focus, equation (1) gives J = 3000, equation (2) gives M = ×2,
and equation (3) gives x = 75mm. [2]
[1] For the purposes of these equations, the focal length
of the Barlow is signed positive. Although I generally use RIP, in this context
I prefer this way of doing things because the introduction of a negative f
tends to lead to more errors. If you wish to use the RIP convention, f
is negative and the equations must be modified accordingly. I will leave that as
an exercise for the interested reader.
[2] Note, from the numerical examples, how a 12.5mm
shift in the Barlow has resulted in a 75mm change in x. This also
explains why, when you use a zoom eyepiece (zoom is essentially a moveable
Barlow), only slight refocusing is required when you change the effective focal
length of the eyepiece.


